The Math Trick Behind MP3s, JPEGs, and Homer Simpson’s Face
Joyce Park stashed this in Science
Stashed in: Simpsons!, Math!, For Milo, For Conrad, About GIFs, Mathy
A beautifully simple explanation of Fourier transforms and why they matter in your daily life.
Cool:
In these images (click through to Wikipedia to see it as an animation), the red squarish wave is distilled into a set of pure notes (the blue sine waves). Think of these blue waves like a mathematical ingredient list for the red wave. Pressing this analogy, the Fourier transform is a recipe—it tells you exactly how much of each note you need to mix together to reconstruct the original wave. The vertical blue lines in the animation are essentially a graph visually representing the amount of each note.
Here’s another way to think about this, provided by Matthew Henderson, or “Matthen,” a Ph.D. student at Cambridge University who also creates animated GIFs of mathematical curiosities. Matthen explains Fourier’s trick using circles instead of sine waves. This involves a set of circles of different sizes, each one centered on the edge of a bigger circle. Then the circles begin to spin, the big circles swinging the smaller ones around, and the smaller ones spinning faster than big ones. If you trace the motion of one point on the smallest circle, you can reconstruct a wave of any shape, as shown in the animation and the stills below. Again, the Fourier transform tells you how to build the wave: which circles, moving at which speeds.


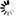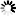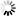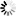








5:20 PM Nov 07 2013