Visualization: Basketball Game Stacks
Mo Data stashed this in Sports Analytics
https://causalsportsfan.wordpress.com/2013/02/05/visualization-basketball-game-stacks/
Visualization: Basketball Game StacksPosted on February 5, 2013 | 4 Comments
Note: On my dad’s advice, I posted another version of the Game Stacks that depicts rebounding rates, rather than just total offensive rebounds. The discussion in this post is a little naive on that point — the new version yields a better analysis of rebounding.
I have a general hang up when looking at the box score for basketball (or listening to announcers list off statistics). I see some rebounding numbers, but I can’t tell who rebounded better without offensive and defensive breakdowns, plus the number of shots missed by each team. And I see shooting percentages and shot attempts, but it’s hard to put it all together into how a team got its points.
I realized that what I really want to see is not complicated. Here’s the list:
- What each team did with their scoring chances:
- Two point attempts
- Three point attempts
- Free throw trips (2 attempts)
- Turnovers
- Efficiency on each type of shot
- Rebounding advantage in terms of extra scoring chances
- And, of course, total score
All these stats exist, but there should be an easy way to see all of it at once and get a sense for how the game was won. Here’s my first try, the Game Stack:
The picture shows total “plays,” or chances to score, for each team, and total points, broken down by type. In a quick glance, you can see that Indiana was out-rebounded (Michigan got three more chances to score) and turned the ball over a ton. However, on just over 60 non-turnover plays, the Hoosiers were extremely efficient. They got to the line much more (a “FT trip” is two shots*), and players shoot a much higher percentage from the line than the field. They also shot a higher percentage than Michigan on two pointers and three pointers. Michigan had well over 70 non-turnover plays, but they were so inefficient (few free throws, low percentage from the field), that they lost by eight points.
Can’t you just here Dick Vitale screaming, “Look at how the teams stack up! The Wolverines, they gotta get the solid boxes as tall as the dotted boxes! You need to average at least one point per shot to compete against a team like Indiana! They’re forcing turnovers and rebounding, but they’re not getting to the line like the Hoosiers are, baby!
If you’re not convinced yet, here’s a good NBA Game Stack from Sunday:
The scoreline was much closer for this one (Lakers win 98-97). However, that scoreline obscures a more interesting story. The Pistons generated six extra chances on the boards, but the Lakers made up the advantage by getting to the line (the high percentage option) and shooting a much better percentage on twos, including a nice three point play for Kobe to win the game . . . come on Pistons!
And one more Stack from Sunday:
Another close game, but this time the road team held the rebounding advantage (no surprise, given that the Celtics don’t really try for offensive rebounds). The Clippers squandered their seven extra chances by committing more turnovers, shooting fewer free throws at a lower percentage, and shooting slightly worse from three. Those disadvantages were just enough to lose, despite a decent efficiency advantage on two pointers.
The key to the Game Stack is that all the insights I’m writing are quickly apparent from a glance, once you get the hang of the diagram. I’d like to list actual shooting percentages and break down the rebounding advantage, too (offensive versus defensive). It might be cool to make an interactive version that pops out some extras like that. You could even imagine expanding each section of the bars and showing which players contributed what to each stat category. Most of all though, I like the Game Stack for its quick summary of how the game was won.
* To avoid digging into play by play data, I used (FT attempts/2) to estimate trips to the line. In reality, college teams take one free throw sometimes on one-and-ones or three if fouled on a three pointer (rare). Extra free throws on and-one opportunities help balance out the one-and-ones (these extras are really part of a two point shot play), so dividing by two probably gets close to the total number of plays (and hence the rebounding advantage is about right). It would certainly be better to nail all this with play by play data, but it wouldn’t make the picture too different for most games.
Stashed in:





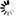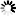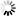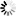







2:52 PM Jul 06 2015